Schubladendenken ist oft verpönt, kognitiv aber dennoch sinnvoll, da das Gehirn so die Komplexität der Welt etwas reduzieren kann, um sich vor einer Überlastung zu schützen. Auch in der Statistik kann man sich eine ähnliche Methodik zunutze machen. In diesem Blogeintrag erklären wir die Logik von Clusteranalysen. Speziell möchten wir den k-Means-Algorithmus vorstellen.
Die Datenmengen in unserer Welt wachsen und wachsen. Das Bewusstsein ist längst geschaffen für den Wert, der in Daten steckt, und den man sich zunutze machen möchte. Diese wachsende Datenmasse erfordert aber auch Möglichkeiten zur Ordnung und Kategorisierung. Ein Weg besteht darin, Zusammenhänge und Ähnlichkeiten zwischen Variablen zu identifizieren und diese entsprechend in Klassen einzuteilen, deren Mitglieder ähnliche Eigenschaften aufweisen. Damit wird aus einer großen Menge von eventuell unübersichtlichen Daten die Möglichkeit geboten, Ballungen zu erkennen und diese stellvertretend für die Einzelbeobachtungen zu betrachten.
Wir möchten in diesem Blogbeitrag ein Verfahren zur Gruppierung (auch Clusterung, Kategorisierung, Klassifikation) näher erläutern, welches diesen Anforderungen gerecht wird: das k-Means-Verfahren. Der besseren Visualisierbarkeit wegen verwenden wir ein zweidimensionales Beispiel. Das erläuterte Grundprinzip des Gruppierungsalgorithmus bleibt aber auch für eine größere Variablenanzahl bestehen.
Zwei Einflussfaktoren, zwei Dimensionen
Unternehmen A betreibt mehrere Filialen in unterschiedlichen Preisgruppen und liefert tagesgenau Daten zum Umsatz und zur Anzahl der Kunden, die seine Filialen besuchen. Aus diesen Daten berechnet sich der durchschnittliche monatliche Umsatz und die durchschnittliche monatliche Kundenzahl (Abbildung 1):
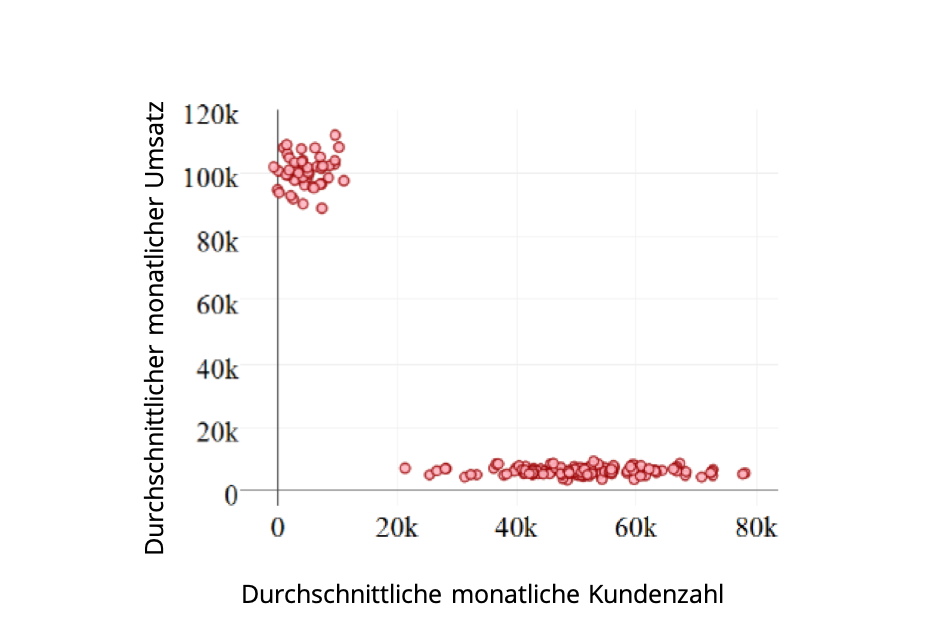
Die Graphik lässt augenscheinlich zwei Gruppen erkennen. Als im Luxuspreissegment verankert kann man die Gruppe definieren, die mit einem geringen Kundenaufkommen einen hohen Umsatz erzielt (Punktwolke oben links). Eine weitere Gruppe im Standardpreissegment erzielt mit einem großen Kundenaufkommen einen relativ kleinen Umsatz (längliche waagrechte Linie). In dem hier aufgezeigten praxisnahen Beispiel kann der Mensch die Kategorisierung durch bloßes Hinschauen selbst vornehmen.
Mehr Einflussfaktoren, mehr Komplexität
Das obige Beispiel zeigt, dass man sich bei der Analyse von einigen wenigen Variablen – in diesem Fall der beiden Variablen „Durchschnittliche monatliche Kundenzahl“ und „Durchschnittlicher monatlicher Umsatz“ – die visuelle Darstellung in 2D- oder (bei drei Variablen) 3D-Scatterplots oft noch sehr gut zunutze machen kann. Das Problem verschärft sich jedoch erheblich, wenn noch andere Kategorisierungsmerkmale wie beispielsweise das Alter der Kunden in die Analyse einfließen, und zweidimensionale Abbildungen den Sachverhalt nicht mehr erfassen können. Spätestens jetzt gibt es gute Gründe für ein maschinenbasiertes Vorgehen bei der Kategorisierung von Daten: Es ist Zeit für die Anwendung eines sogenannten Clusterverfahrens. Im Machine-Learning-Kontext gehören solche Verfahren zu den Unsupervised-Learning-Verfahren. Unter dem Begriff „Cluster“ versteht man hierbei eine durch das Verfahren ermittelte Gruppe von Datenpunkten.
Ein Clusteralgorithmus, ein Mittel gegen die Komplexität
Der k-Means-Algorithmus ist ein häufig verwendetes Verfahren der Clusteranalyse (Forgy, 1965; MacQueen, 1967). Das Verfahren lässt Zentren von Clustern bestimmen, die dazu genutzt werden können, neue Datenpunkte in eine bestehende Gruppenstruktur einzupassen.
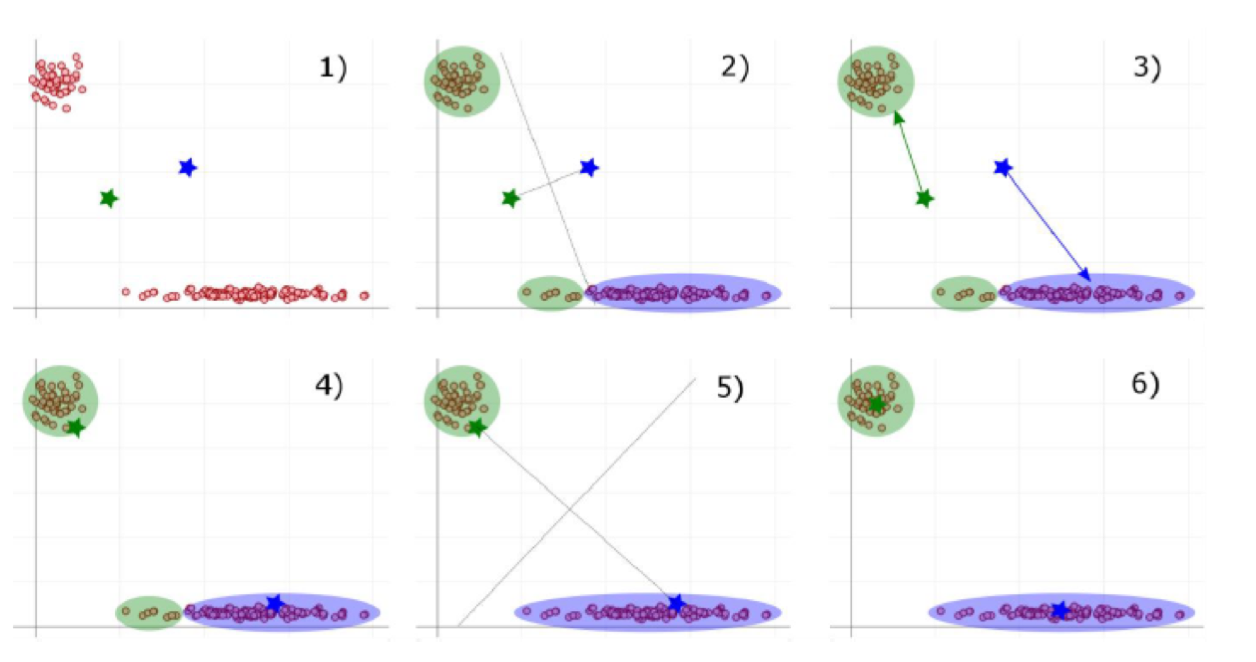
Im Beispiel unseres Unternehmens A zeigt der erste Schritt des Verfahrens in Abbildung 2, wie k = 2 Gruppenzentren zufällig im Koordinatensystem der vorhandenen Datenpunkte verteilt werden (grüner und blauer Stern in 1) von Abbildung 2). Dann erfolgt die Zuordnung über den kürzesten Abstand des jeweiligen Datenpunkts zu einem der beiden Zentren (der euklidische Abstand wird hier als kanonisches Beispiel verwendet, wobei andere Abstandsarten auch denkbar sind). Die Mittelsenkrechte (gepunktete Linie in Abbildung 2) gilt hierbei als imaginäre Trennlinie. Wenn die Datenpunkte einem Zentrum zugeordnet sind, werden die Gruppenzentren zum Schwerpunkt dieser neu gefundenen Gruppe verschoben (Schritte 3) und 4) in Abbildung 2).
Danach wiederholen sich die Schritte 1) bis 4) so lange, bis keine Datenpunkte die Gruppenzuordnung mehr wechseln, d. h. kein Farbwechsel mehr stattfindet. Im hiesigen Fall ist dies bereits nach der zweiten Iteration des Verfahrens der Fall: Falls man nun ausgehend von Schritt 6) versuchen würde, den Algorithmus weiter anzuwenden, würde sich an der Gruppenzuordnung nichts mehr ändern.
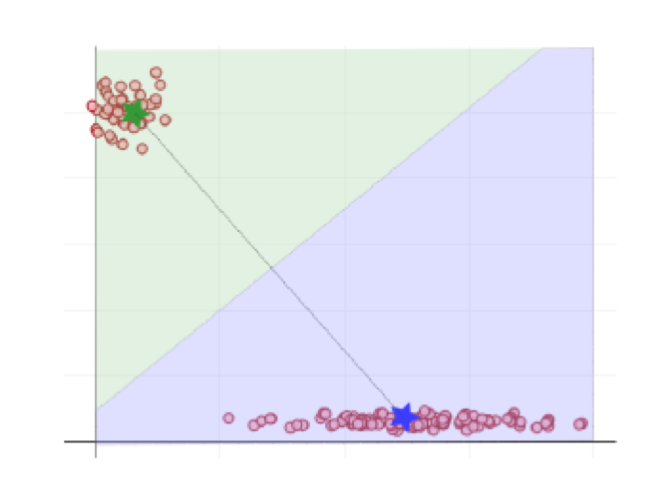
In Abbildung 3 ist das Endergebnis des Algorithmus dargestellt. Aus der Position der errechneten Clusterzentren resultieren die abgebildeten Flächen, welche die Zugehörigkeit aller möglichen Datenpunkte markieren. Das bedeutet: Wenn ein neuer Datenpunkt, beispielsweise eine neue Filiale, in das System einbezogen werden soll, befindet er sich automatisch in der grünen oder blauen Fläche. Damit ist er eindeutig kategorisiert beziehungsweise einer Gruppe zugeordnet. Der Maschine wurde beigebracht, selbstständig Daten zu kategorisieren.
Treffende Maßnahmen, treffende Ergebnisse
Was macht man nun mit dem Ergebnis? Man weiß nun also, dass es zwei Cluster gibt, wobei ein Cluster viele Kunden mit relativ wenig Umsatz umfasst und das andere deutlich weniger, aber deutlich zahlungskräftigere Kunden. Der Anwendungsfall legt nahe, dass eine bestimmte Filiale des Unternehmens eindeutig einem der beiden Cluster zuzuordnen ist, und somit entweder zum Luxuspreissegment oder zum Standardpreissegment gehört. (Streng genommen wäre das noch zu prüfen.) Dementsprechend können nun beispielsweise separat für die beiden Cluster Marketingmaßnahmen geplant werden, die gezielt das jeweilige Cluster ansprechen. Auch können Dienstpläne für die Angestellten gestaltet werden, die in den verschiedenen Filialen mit unterschiedlich viel Kundenzulauf zu rechnen haben. Aufgrund der unterschiedlichen Zielgruppen und Sortimente bedürfen diese sicherlich auch unterschiedlicher Schulungen. Die Tatsache, dass es nicht mehr Cluster als Preissegmente gibt, bestätigt zudem, dass es tatsächlich genügt, die Luxusfilialen und Standardfilialen jeweils gesammelt zu betrachten, und hier nicht noch eine weitere Unterscheidung nötig ist.
Nicht immer sieht die Realität so schön und naheliegend aus wie in unserem Beispiel, aus dem man auch auf einfachere Art und Weise, z. B. visuell, und mit gesundem Menschenverstand gewisse Erkenntnisse hätte ziehen können. Aber genau da können einem solche Clusterverfahren potenziell Zusammenhänge und Erkenntnisse liefern, die bisher unbekannt waren, die überraschen können und echten Mehrwert bringen. Im Übrigen ist auch die resultierende Anzahl an Clustern i. A. alles andere als naheliegend und ihre Wahl eine Sache für sich, worauf wir hier aber nicht näher eingehen werden.
Zeitreihen clustern, Zeitreihen vorhersagen
Bevor wir schließen, möchten wir noch die Frage beantworten, was Clusteranalysen mit Predictive Analytics zu tun haben. Häufig trifft man sie als Vorstufe zur eigentlichen Prognosemodellbildung an. Mit ihrer Hilfe kann man zum Beispiel Erkenntnisse darüber gewinnen, welche Ähnlichkeiten es in einer großen Menge an potenziellen Einflussfaktoren einer Zeitreihe gibt und wie man daraus eine geeignete Variablenvorauswahl für das Prognosemodell treffen könnte. Eine andere Möglichkeit ist, verschiedene vorherzusagende Zeitreihen mittels eines Clusterverfahrens zu gruppieren, und diese Zeitreihen aufgrund ihrer Ähnlichkeit schließlich ähnlich zu behandeln. So könnte man sich beispielsweise dazu entschließen, pro Cluster nur bestimmte Vorhersagemethoden auf die Zeitreihe anzuwenden oder ausschließlich eine bestimmte Auswahl an Einflussfaktoren in Betracht zu ziehen. Die Liste an Einsatzmöglichkeiten von Clusteranalysen im Bereich Predictive Analytics ist hier aber sicher längst nicht zu Ende. Teilen Sie uns gerne Ihre Ideen und Anregungen mit. Ihre Gedanken dürften ja jetzt ausreichend gut sortiert sein.
Sie haben selbst Lust bekommen, Zeitreihen vorherzusagen? Testen Sie unsere Forecasting-Software future!
Infobox:
Iteration: Iteration beschreibt einen Prozess mehrfachen Wiederholens gleicher oder ähnlicher Handlungen zur Annäherung an eine Lösung oder ein bestimmtes Ziel.
Einflussfaktoren: Unter einem Einflussfaktor versteht man in einem (statistischen) Vorhersagemodell eine Einflussgröße, die als Prädiktor fungiert, also potenziell Einfluss auf die vorherzusagende, abhängige Variable hat und daher in einem Vorhersagemodell berücksichtigt wird. So kann beispielsweise die Tageshöchsttemperatur eine Einflussgröße (Kovariate) für die Modellierung und Vorhersage des täglichen Stromverbrauchs einer Stadt sein.
Unsupervised Learning: Unsupervised Learning ist ein Teilbereich der künstlichen Intelligenz. Im Gegensatz zum Supervised Learning gibt es hier keine abhängige Variable (Zielvariable), die modelliert werden soll. Neben Clustering ist die Dimensionalitätsreduktion (Komprimierung) von Daten das häufigste Ziel von Unsupervised-Learning-Verfahren.
Literaturnachweis:
Forgy, E. (1965). Cluster anlysis of multivariate data: efficiency versus interpretability models. Biometrics, 21(3), 768-769.
MacQueen, J. (1967). Some methods for classification and analysis of multivariate observations. In Proceedings of the fifth Berkeley symposium on mathematical statistics and probability, 1(14), 281-297.