Wenn man auf Grundlage von Daten einen Blick in die Zukunft werfen und Prognosen erstellen möchte, ist es natürlich sinnvoll, wissenschaftlich etablierten Standards zu folgen. Mit welcher Qualität man bei den jeweiligen Prognosen dann rechnen kann, ist dennoch im Vorhinein gar nicht so einfach zu sagen. Wir beschreiben Best Practices, wie man die Prognosegüte im Einzelfall bewerten kann.
Noch vor Beginn eines Projekts und einer Zusammenarbeit werden wir manchmal gefragt: “Welche Prognosegüten könnt ihr denn erreichen?” Und das noch bevor wir überhaupt irgendwelche Daten gesehen haben. So gern wir etwas anderes antworten würden, lautet die einzig plausible Antwort in diesem Fall: “Das wissen wir erst, wenn wir es ausprobiert haben.” Denn jeder Anwendungsfall ist anders. Auf sehr detaillierten Ebenen, z. B. der Vorhersage von wöchentlichen Materialbedarfen, wird beispielsweise oft eine geringere Prognosegüte erzielt als auf der aggregierten Ebene, wenn es darum geht, die Umsätze eines ganzen Unternehmensbereichs auf Monatsebene vorherzusagen. Da wäre es schlicht Kaffeesatzleserei, würden wir von vornherein sagen: “Wir können eine Prognosegüte von 92 % erzielen.” Natürlich haben wir aus Erfahrung mit anderen Unternehmen und Projekten eine Idee, wie gut es im vorliegenden Fall funktionieren könnte. Aber sicher wissen kann man es vorher in der Regel nicht.
Vor allem ist es nicht nur eine Frage der ausgefeiltesten Vorhersagemethoden und -techniken, wie genau die Vorhersagen letztendlich sind. Zusätzlich entscheidet auch schlicht die einem Phänomen innewohnende Volatilität darüber, wie gut das Phänomen vorhersagbar ist. Hinzu kommt, dass sich die Prognosegüte über die Zeit auch verändern kann. Besondere Phasen der Unsicherheit lassen es oft nicht zu, die gleiche Prognosegüte zu erreichen, als wenn man sich in einer stabilen Phase befände.
Prognosegüte als Gegenstück zum Fehlermaß
Es gilt also, die Prognosegüte in Zahlen zu fassen. Aus einem initial nur guten Gefühl wird so eine stichhaltige Überzeugung über die Genauigkeit von Vorhersagen. Es lassen sich verschiedene Vorhersagetechniken und -anbieter miteinander vergleichen und man bekommt einen besseren Eindruck von dem, was im vorliegenden Fall diesbezüglich überhaupt möglich ist. Denn Fakt ist: Mit dem Erstellen von Forecasts alleine ist es nicht getan.
Es gibt Ansätze, die man als Best Practices der Vorhersagegüte-Messung bezeichnen kann. Doch wie bereits angedeutet: Unterschiedliche Anwendungsfälle verlangen unter Umständen nach unterschiedlichen Berechnungsmethoden.
Die Güte von Vorhersagen zu beurteilen, geht aus zweierlei zeitlichen Perspektiven:
- live, d.h. man verfolgt mit, wie gut sich entstandene Forecasts im Live-Betrieb schlagen. Man nennt dies auch Forecast-Monitoring.
- rückblickend, d.h. man fragt sich, wie gut eine Vorhersagetechnik oder ein -modell denn abgeschnitten hätte, hätte man es bereits seit einiger Zeit angewendet. Mittels dieses sogenannten Backtestings stellt man das Modell i.d.R. noch vor einer Live-Anwendung auf den Prüfstand. Somit spielt es bei der Beurteilung von Forecasts und der Auswahl eines Vorhersagemodells eine wichtige Rolle.
Der Prognosefehler misst, wie viel sich eine Prognose verschätzt.
Ob man die Forecasts nun rückblickend oder im laufenden Betrieb beurteilen möchte: Beiden Perspektiven liegt dasselbe Grundprinzip zu Grunde:
- Von einem bestimmten Zeitpunkt aus erzeugt man einen Forecast für einen Zeitpunkt in der Zukunft.
- Man betrachtet den eingetretenen Wert zu diesem Zeitpunkt in der Zukunft. Im Falle des Forecast-Monitorings muss man abwarten, bis dieser Zeitpunkt überhaupt eingetreten ist. Im Falle des Backtestings liegt dieser bereits vor.
- Man vergleicht den eingetretenen Wert mit dem zuvor getätigten Forecast. Die Differenz aus beiden Größen nennt man Prognosefehler.
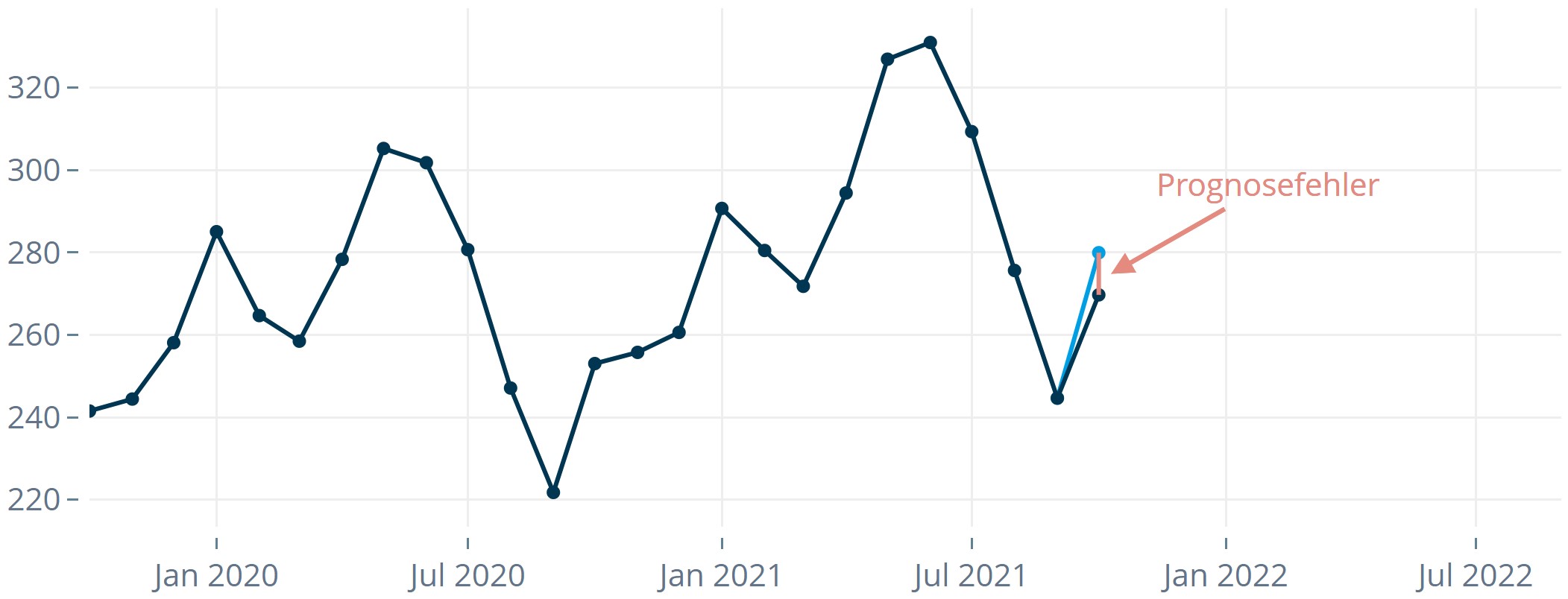
Der Prognosefehler zum Zeitpunkt i – die Differenz zwischen tatsächlichem Wert (acti) zum Zeitpunkt i und Forecast (fci) zum Zeitpunkt i – ist Grundlage der meisten Maße, mit Hilfe derer man die Güte der Vorhersagen beurteilt.
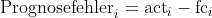
Der in Abbildung 1 gezeigte Fehler ist ein 1-Schritt-Prognosefehler. Er beruht auf den 1-Schritt-Prognosen, d.h. es wird von einem Zeitpunkt aus genau ein Zeitintervall (z. B. einen Monat) weit in die Zukunft geschaut. Es lassen sich aber auch höhere Prognoseschritte auswerten. Beispielsweise ist Ende Juli die Produktionsplanung für August bei vielen Unternehmen längst abgeschlossen. Stattdessen rückt die Produktion für Oktober bereits in den Planungsfokus, man interessiert sich also ganz besonders für die 3-Schritt-Prognose. In diesem Fall bietet es sich an, besonderes Augenmerk auf die Auswertung der Prognosegüte für die 3-Schritt-Prognose zu legen. Ziel einer Optimierung ist es dann, den 3-Schritt-Prognosefehler zu minimieren.
Die Fehlermaße, die wir im Folgenden auflisten, lassen sich für 1-Schritt-Prognosen sowie auch für höhere Vorhersageschritte auswerten.
Backtesting: Weil man im Nachhinein eben immer schlauer ist.
Um eine zuverlässige Aussage über die Forecasting-Strategie zu bekommen, schaut man sich üblicherweise nicht nur an einem einzigen Zeitpunkt Vorhersagen und wahre Werte an, sondern über einen längeren Zeitraum. Im Rahmen dieses sogenannten Backtestings werden Vorhersagen für einen vergangenen Zeitraum simuliert, z. B. für das zurückliegende Jahr. Man kann sich dann zunutze machen, dass man die tatsächlich eingetretenen Werte bereits kennt, und Vergleiche zwischen Forecasts und tatsächlichen Werten anstellen. Dabei geht man im Zeitreihenkontext im Wesentlichen folgendermaßen vor:
- Man unterteilt die gegebene Datenhistorie in einen Trainingszeitraum und einen Testzeitraum (Backtesting-Zeitraum).
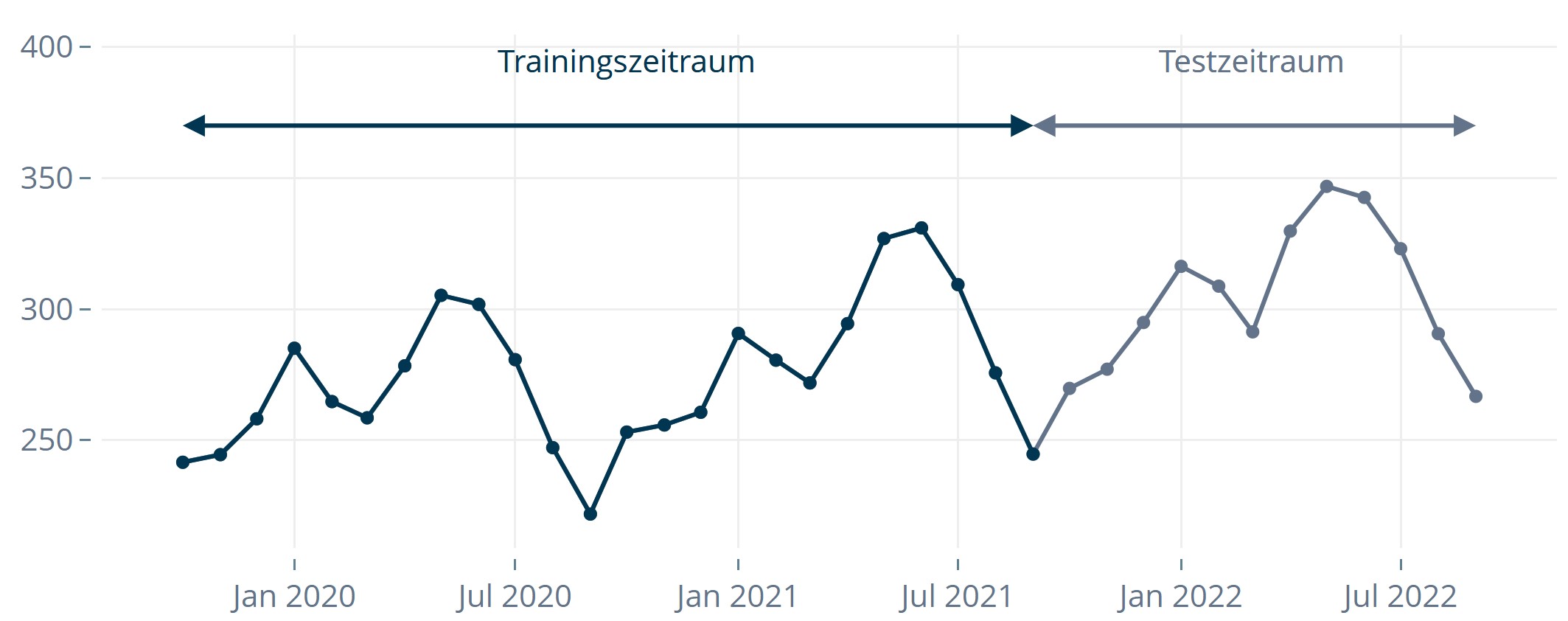
Abbildung 2: Einteilung in Trainings- und Testzeitraum
- Man macht eine Vorhersage für den ersten Zeitpunkt im Testzeitraum und stellt sich dabei vor, man kennt nur die bis zu diesem Zeitpunkt zurückliegenden Beobachtungen.
Abbildung 3: Mit dem auf dem verkürzten Datensatz trainierten Modell wird eine Prognose erstellt.
- Anschließend macht man eine Vorhersage für den zweiten Zeitpunkt im Testzeitraum und stellt sich vor, nur die bis dahin zurückliegenden Informationen seien vorhanden.
- Usw. bis zum letzten Zeitpunkt im Testzeitraum.
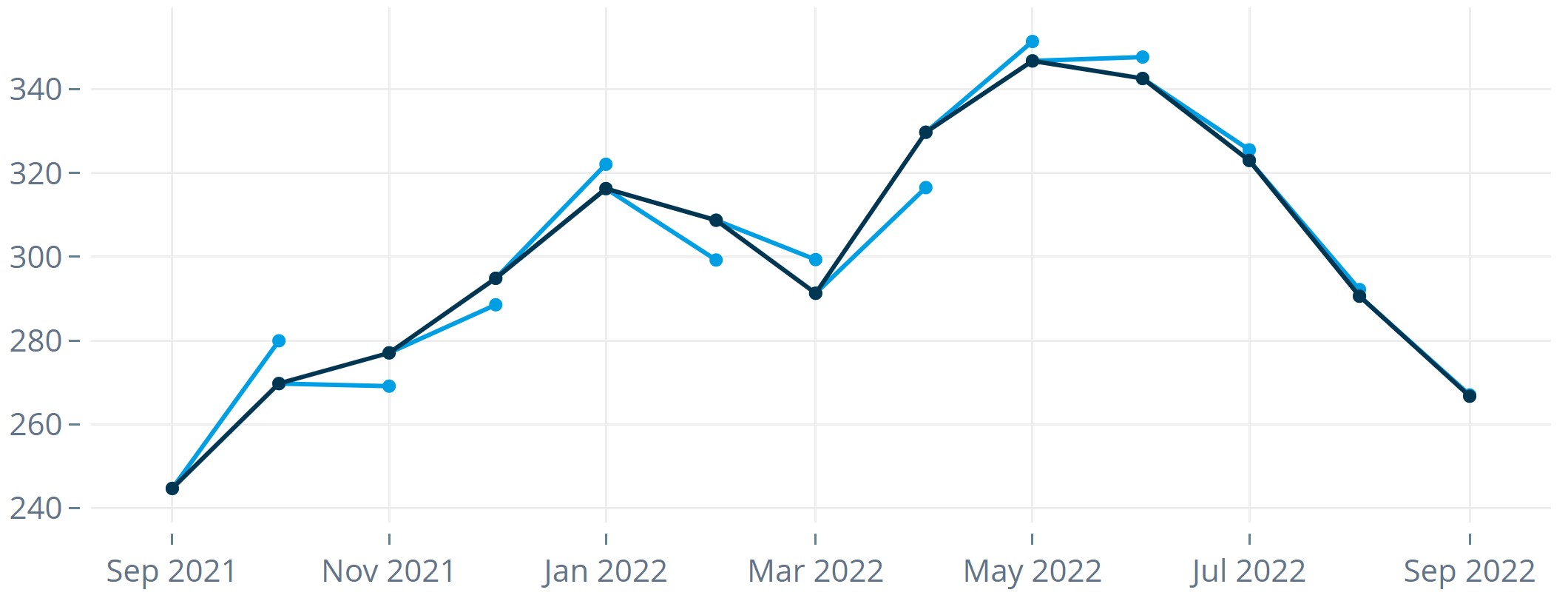
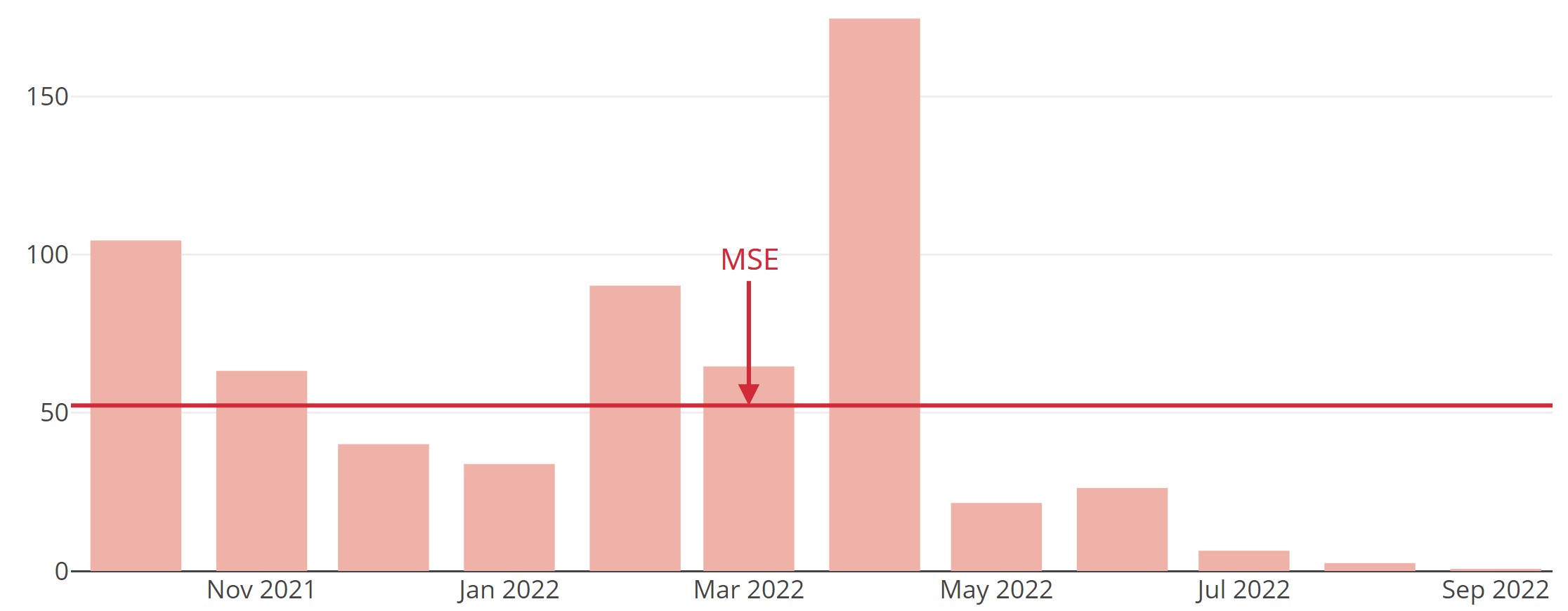
Abbildung 4: Forecasts und tatsächliche Werte im Verlauf eines Backtesting-Zeitraums von n = 12 Monaten. - Man ermittelt für alle Zeitpunkte im Testzeitraum die Prognosefehler.
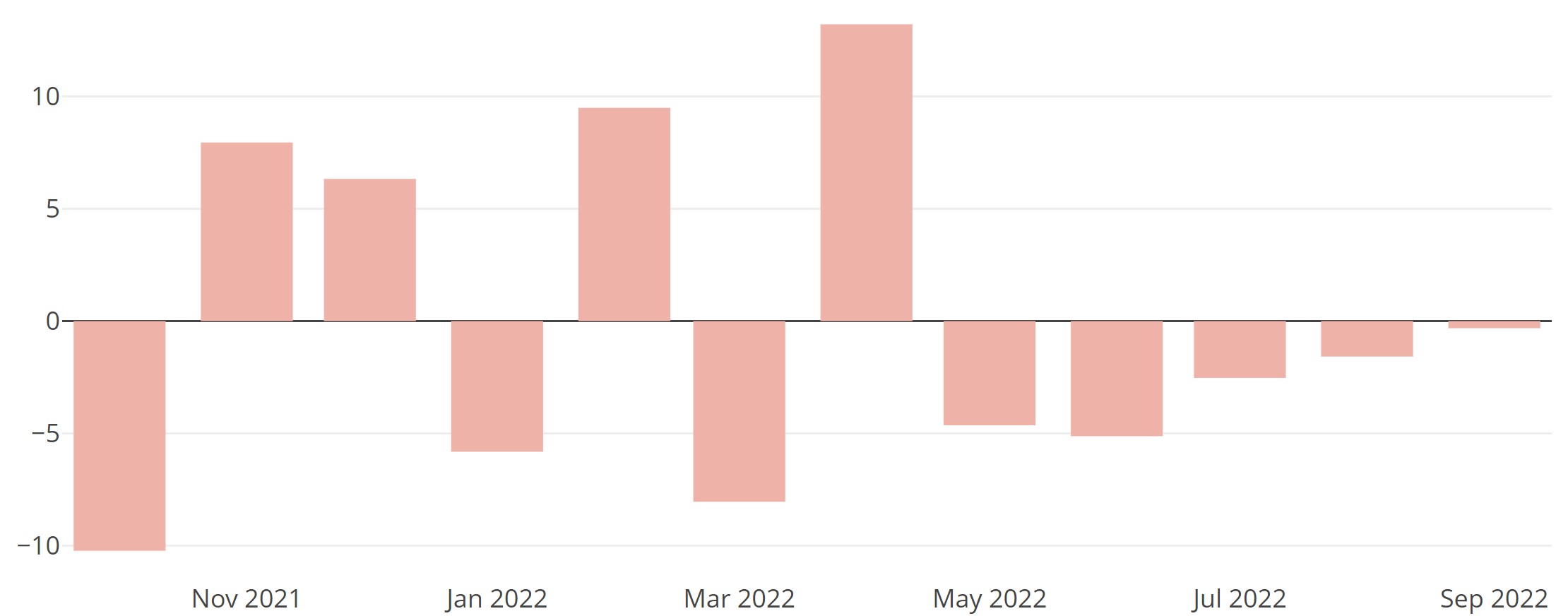
Abbildung 5: Prognosefehler im Verlauf eines Backtesting-Zeitraums von n = 12 Monaten. - Man ermittelt auf Basis der Prognosefehler (und Forecasts) einen aussagekräftigen Wert, der diese geeignet zusammenfasst bzw. verdichtet. Man erhält ein Fehlermaß, welches eine Aussage darüber liefert, wie gut oder schlecht die Vorhersagen abschneiden.
Fehlermaße verdichten die Prognosefehler.
Um die Güte eines Modells zu beurteilen, kann man unterschiedliche Güte- bzw. Fehlermaße konstruieren oder heranziehen. Die meisten dieser Maße basieren auf einer Auswertung der Prognosefehler. Wir werden in diesem Blogbeitrag ausgewählte vorstellen, aber keine vollständige Liste liefern, alleine schon deswegen, weil es sehr viele davon gibt. Wir möchten aber ein paar Beispiele aus verschiedenen Kategorien bzw. für verschiedene Anwendungsfälle aufzeigen und erhoffen uns dadurch nicht zuletzt, dass wir eine Sensibilität dafür schaffen können, welche Bedeutung und Anwendungsmöglichkeiten diese Maße haben. Einige können in einer bestimmten Situation nämlich total angemessen, in einer anderen wiederum völlig unpassend sein.
Wir beschreiben im Folgenden Fehlermaße, die tatsächlich nicht bewerten, wie gut eine Prognose ist, sondern wie schlecht. Prognosegüte ist dann das positiv formulierte Pendant zu Fehlermaß. Auch hierfür gibt es die eine oder andere Formel. Beispielsweise messen manche Unternehmen Prognosegüte als 100 % - MAPE (s. u.). Wir konzentrieren uns aber, wie gesagt, auf die Fehlermaße, für die gilt: Je näher sie sich an null befinden, desto besser.
ME (“Mean Error”, engl. für “mittlerer Fehler”)
Das naheliegendste und am einfachsten zu bestimmende Fehlermaß bildet aus den n ermittelten Prognosefehlern in einem Backtesting-Zeitraum einen Durchschnitt: den ME.
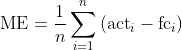
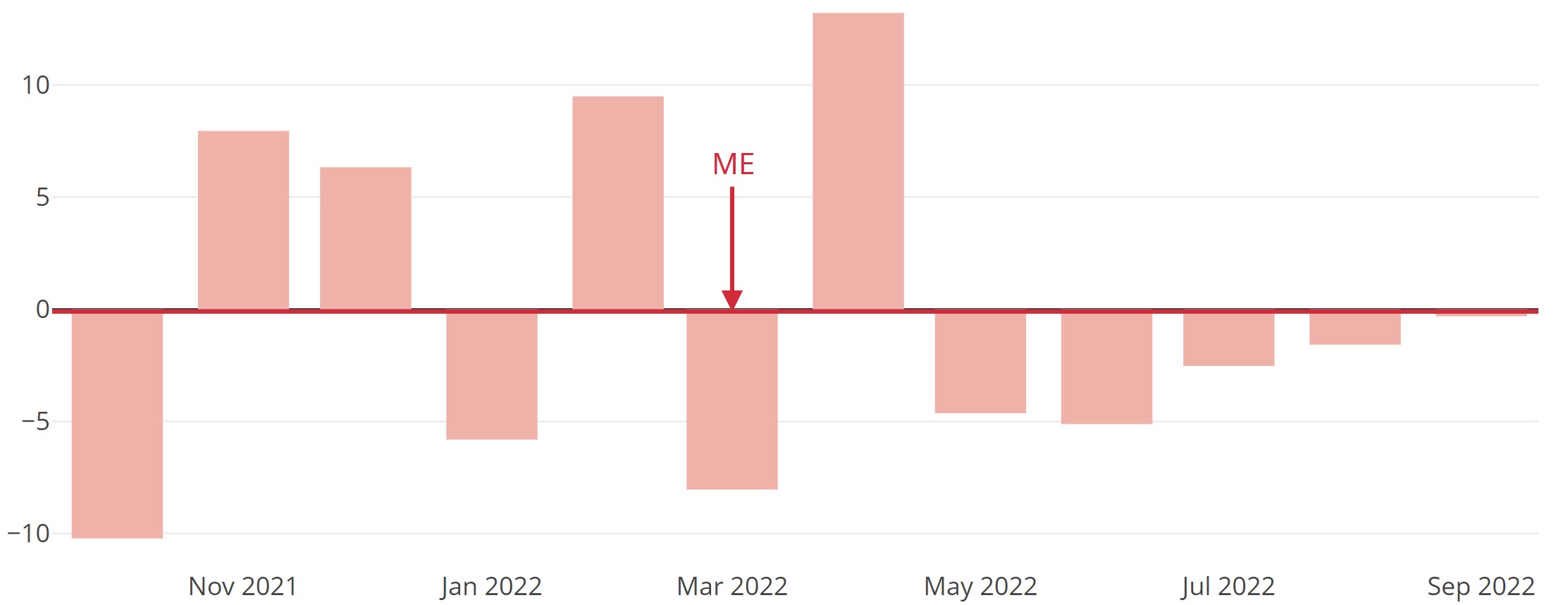
Der ME ist sensitiv gegenüber den Vorzeichen der Prognosefehler. Wenn er unter null liegt, wurde beim Forecasting volumenmäßig mehr unter- als überschätzt. Entsprechendes gilt umgekehrt. Wenn im Extremfall die Hälfte der wahren Werte um x Einheiten unterschätzt und die andere Hälfte um genauso viele Einheiten überschätzt wurde, beträgt der ME null. Trotzdem lag der Forecast für alle Zeitpunkte potenziell gewaltig daneben.
MAE (“Mean Absolute Error”, engl. für “Mittlerer absoluter Fehler”)
Um dem Problem zu entgehen, dass sich Über- und Unterschätzen gegenseitig aufheben können, betrachtet man mit dem MAE den Durchschnitt der absoluten Prognosefehler.
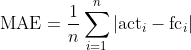
MSE (“Mean Squared Error”, engl. für “Mittlerer quadratischer Fehler”)
Weil man große Prognosefehler gerne stärker bestraft als kleine, geht man oft noch einen Schritt weiter und quadriert die Fehler vor der Durchschnittsbildung, was zum MSE führt.
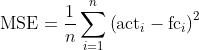Durch das Quadrieren erreicht man auch in diesem Fall, dass das Vorzeichen der Prognosefehler ignoriert wird. Der MSE gehört zu den beliebtesten Maßen zur Beurteilung der Prognosegüte und wird aufgrund seiner Eigenschaften in der Statistik auch an vielen anderen Stellen, z. B. als Optimierungskriterium bei der linearen Regression, eingesetzt. Allerdings ist der MSE durch das Quadrieren auch anfälliger gegenüber Ausreißern als der MAE.
Anstelle des MSE wird gerne auch der RMSE (“Root Mean Squared Error”, engl. für “Wurzel aus dem mittleren quadratischen Fehler”) angegeben. Vorteil ist, dass man sich bzgl. der Einheit des Maßes wieder in bekannten Gefilden aufhält, man also bei der Vorhersage von Umsätzen, die z. B. in EUR gemessen werden, nicht mehr mit EUR2 wie beim MSE zu tun hat, sondern mit EUR.
MAPE (“Mean Absolute Percentage Error”, engl. für “Mittlerer absoluter prozentualer Fehler”)
Prognosefehler ebenso wie die oben vorgestellten Fehlermaße ME, MAE und MSE sind nicht skalenunabhängig. Das bedeutet, dass sie stets in Relation zur Größenordnung der vorhergesagten Größe zu interpretieren sind. Eine Abweichung von 100 Stück bei der Vorhersage beispielsweise der verkauften Menge an Produkten mag akzeptabel sein, wenn sich die verkaufte Menge in der Größenordnung von mehreren 10.000 Stück bewegt, aber nicht unbedingt, wenn sie sich für gewöhnlich im Bereich um 10 bis 1000 aufhält. Um unabhängig von der Skala ein Gefühl dafür zu bekommen, ob die Abweichungen groß oder klein sind, nimmt der MAPE die Relation zu den tatsächlich eingetretenen Werten in Betracht. Erst werden die prozentualen Prognosefehler bestimmt. Dann werden sie vom Vorzeichen bereinigt und gemittelt.
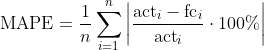
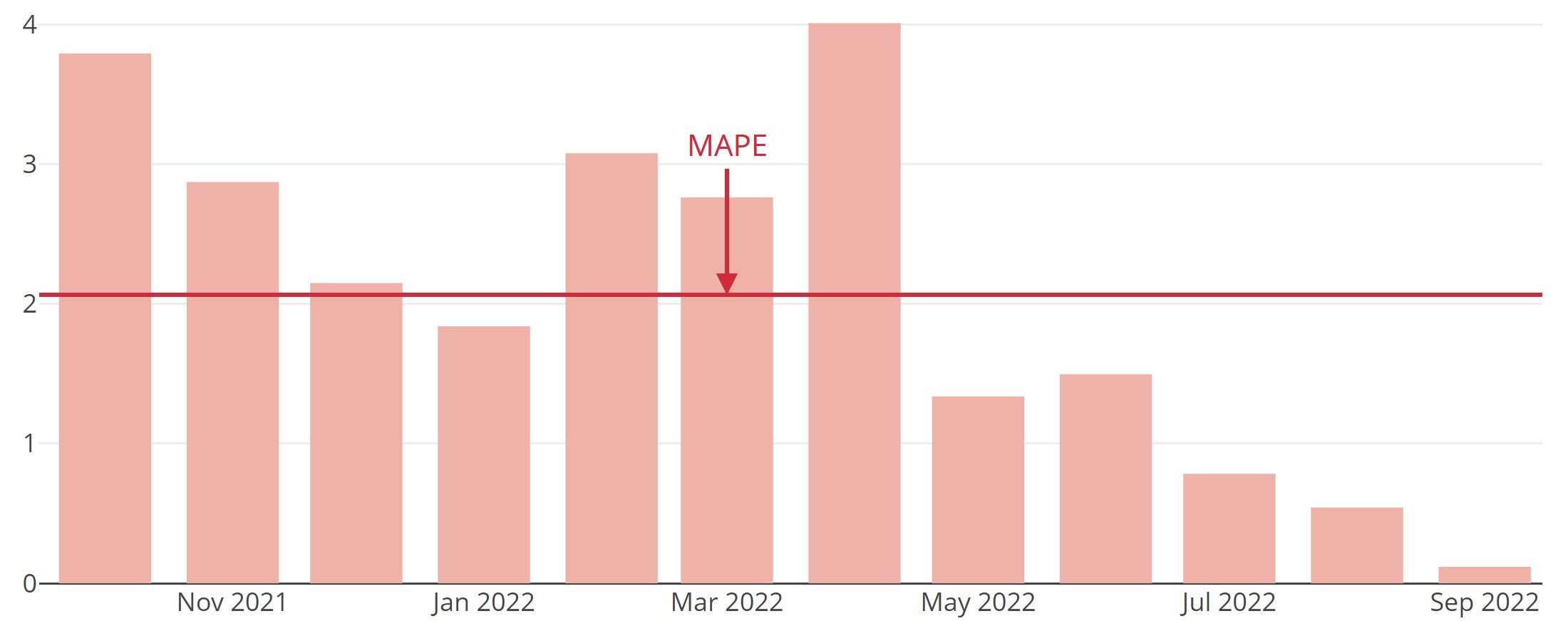
PIS (“Periods in Stock”, engl. für “Zeiteinheiten im Lager”)
Periods in Stock (PIS) ist ein Fehlermaß, das aufsummiert, wie lange Prognosefehler als Bestand in einem fiktiven Lager bleiben, bis sie durch entsprechende Prognosefehler in die andere Richtung ausgeglichen werden. Somit ist bei diesem Fehlermaß die Richtung der Abweichung von Bedeutung.
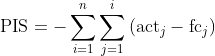
PIS bezieht des Weiteren die Dauer des Mismatches zwischen Prognose und tatsächlichem Wert mit ein, was die oben vorgestellten Fehlermaße nicht tun. Daher kann er gut zur Bewertung von Prognosen von sporadischen Zeitreihen, also Zeitreihen mit vielen Nullwerten, verwendet werden. Solche Zeitreihen kommen oft vor, wenn man beispielsweise auf sehr detaillierter Ebene die Nachfrage nach Artikeln analysiert, die in manchen Zeiteinheiten auch einfach mal nicht vorhanden ist. Das betrifft Anwendungsfälle, in denen Lagerhaltung eine Rolle spielt und i.d.R. nicht-negative Werte anfallen. Der (ansonsten sehr beliebte) MAPE ist in diesem Fall kein geeignetes Maß, da man bei seiner Verwendung durch null teilen müsste. Der PIS wurde von Wallström und Segerstedt (2010) eingeführt.
Beispiel: Eine Prognose mehrere Tage zu früh (Prognose 1) führt zu einem höheren PIS, also einer schlechteren Prognosegüte, als eine um einen Tag verschobene Prognose (Prognose 2), während andere Fehlermaße wie der MAE beide Fälle gleich bewerten:
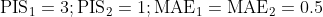
Höhere Vorhersageschritte spielen bei der Bewertung der Prognosegüte oft die wichtigere Rolle als kleine.
Die 1-Schritt-Prognosefehler bekommen in der Modellbildung meist die größte Aufmerksamkeit. In der Praxis jedoch sind die höheren Vorhersageschritte oft sogar deutlich relevanter als die kurzfristigen. Häufig ist es sogar so, dass ein Unternehmen nicht nur einen Prognoseschritt ganz besonders intensiv betrachtet, sondern mehrere auf einmal. In diesem Fall kann sogar eine geeignete Aggregation der Fehlermaße dieser verschiedenen Prognoseschritte sinnvoll sein. Welche Prognoseschritte konkret besonders wichtig sind und welche Art der Aggregation sich anbietet, ist sehr individuell und hängt von den Prozessen des jeweiligen Unternehmens und der speziellen Anwendung ab.
Beispiel: Ein Unternehmen plant die Produktion i.d.R. mit einem Vorlauf von drei bis vier Monaten. Die Planwerte für die 1- und 2-Schritt-Prognosen haben für das Unternehmen keine große Relevanz mehr, da alle Maßnahmen für die Produktion bereits eingeleitet sind. Die Planzahlen für den kommenden und den darauf folgenden Monat wurden also längst “eingefroren”. Höchst relevant für die Produktionsplanzahlen sind jedoch die Vorhersagen für drei und vier Monate in die Zukunft. Für das Unternehmen ist daher ein gewichtetes Mittel zwischen dem RMSE der 3-Schritt-Prognose und dem RMSE der 4-Schritt-Prognose für die Bewertung der Prognosegüte interessant.
Ein Prognosegüte-Maß muss zum Anwendungsfall passen.
Es zeigt sich: Jedes Unternehmen tickt bei jedem Anwendungsfall ein bisschen anders. Bei sporadischen Nachfragemustern kann man den MAPE beispielsweise nicht anwenden. Umgekehrt passt der PIS nicht zu voluminösen, sehr aggregierten Zeitreihen ohne Nullwerte. Zudem hat jedes Unternehmen etwas andere Planungsprozesse, misst also auch immer mit etwas anderem Maß.
Generell ist es äußerst empfehlenswert, ob als Data Scientist oder AnwenderIn, sich die Frage nach der Vorhersagegüte zu stellen. Denn wer als Data Scientist beobachtet, zurückblickt und hinterfragt, ist sich seiner Sache sicherer, lernt dazu oder kann, falls nötig, Verbesserungen an der Forecast-Strategie vornehmen. Als AnwenderIn hat man auf diese Weise fundierte Zahlen für das Management oder Vergleichswerte zu einem Benchmark parat.
Wer die Frage, ob es sich um gute Forecasts handelt, eher qualitativ beantworten möchte, ist mit Kriterien dieser Art gut aufgehoben: Sind die Vorhersagen durch ein State-of-the-art-Vorhersagemodell entstanden? Ist die Berechnung nachvollziehbar oder zumindest reproduzierbar? Gehen die richtigen und alle relevanten Informationen ins Erstellen der Forecasts ein? In diesem Blogbeitrag findet sich eine Liste an Kriterien, was einen guten Forecast ausmacht.
Verweise
Wallström, P., Segerstedt, A. (2010). Evaluation of forecasting error measurements and techniques for intermittent demand. International Journal of Production Economics 128(2), 625–636.
Sie stellen sich die Frage, welche Prognosegüte in Ihrem Anwendungsfall und für Ihre Daten erzielbar ist? Testen Sie es kostenlos!